PART A: MATLAB practice.
1. Open MATLAB. Open the editor and copy paste the following code. Name your code as FirstCode.m
Save the resulting plot as a JPEG image and put it here.
clear all;
close all;
x = [1 2 3 4 5];
y = 2.^x;
plot(x, y, 'LineWidth', 6)
xlabel('Numbers', 'FontSize', 12)
ylabel('Results', 'FontSize', 12)
2. What does clear all do?
Clear all simply clears the command window.
3. What does close all do?
Close all clears the command window and closes all MATLAB figures and graphs etc.
4. In the command line, type x and press enter. This is a matrix. How many rows and columns are there in the matrix?
There is one row and 5 columns in the matrix x.
x =
1 2 3 4 5
5. Why is there a semicolon at the end of the line of x and y?
The semicolon keeps the x and y from being displayed in the command window when the code is ran.
6. Remove the dot on the y = 2.^x; line and execute the code again. What does the error message mean?
It means that with out the period multiple values of x and y cannot be calculated.
7. How does the LineWidth affect the plot? Explain.
This is how thick the line on the plot is going to be.
8. Type help plot on the command line and study the options for plot command. Provide how you would change the line for plot command to obtain the following figure (Hint: Like ‘LineWidth’, there is another property called ‘MarkerSize’)
x = [1 2 3 4 5];
y = 2.^x;
plot(x,y,'r-o','Linewidth',5,'markersize',15)
xlabel('Numbers', 'FontSize', 12)
ylabel('Results', 'FontSize', 12)
9. What happens if you change the line for x to x = [1; 2; 3; 4; 5]; ? Explain.
For this code, the array for "x" becomes a vertical one instead of a horizontal one; ie., there is one column with 5 rows instead of 5 columns with one row. The corresponding output is shown below:
x =
1
2
3
4
5
However, this change in the x array does not change the values for "y" and thus the plot remains the same.
10. Provide the code for the following figure. You need to figure out the function for y. Notice there are grids on the plot.
plot(x,y,'k:s','Linewidth',5,'markersize',15)
xlabel('Numbers', 'FontSize', 12)
ylabel('Results', 'FontSize', 12)
x
GridLineStyle = '--'
grid on
11. Degree vs. radian in MATLAB:
a. Calculate sinus of 30 degrees using a calculator or internet.
The calculated value of sin 30 is .5.
b. Type sin(30) in the command line of the MATLAB. Why is this number different? (Hint: MATLAB treats angles as radians).
MATLAB uses radians as a default measurement and if the user wants degrees they just have to change the code a bit. Below, the code and the output are displayed for "sin(30)."
>> sin(30)
ans =
-0.9880
c. How can you modify sin(30) so we get the correct number?
Using just "sin" will be accurate for values in radians, but to get values for degrees, "sind" can be used instead. The MATLAB input and output are displayed here:
>> sind(30)
ans =
0.5000
12. Plot y = 10 sin (100 t) using Matlab with two different resolutions on the same plot: 10 points per period and 1000 points per period. The plot needs to show only two periods. Commands you might need to use are linspace, plot, hold on, legend, xlabel, and ylabel. Provide your code and resulting figure. The output figure should look like the following:
Graph: Sinusoidal curve of how the coarse would normally appear
To obtain this graph, the following code was entered into MATLAB:t=linspace(0,4*pi/100,10);
y=10.*sin(100.*t);
plot(t,y,'r-o')
hold on
t2=linspace(0,4*pi/100,1000);
y2=10.*sin(100.*t2);
plot(t2,y2,'k')
xlabel('Time (s)')
ylabel('y function')
legend('Coarse','Fine')
Note that the upper value of the linspace command for the two different t values is 4*pi/100. this is because the graph is of the first 2 periods and the period of a sinusoidal function is 2pi/b where "b" is the coeffecient of "t" in the sin function (y=Asin(bt)). So, to show two periods, 2pi/ b was multiplied by 2 to get 4pi/100.
13. Explain what is changed in the following plot comparing to the previous one.
Graph: Function with a maximum value of 5, and what it would normally look like
So for the updated graph, the fine value has a set maximum of 5 now, as opposed to the original function that had a maximum value of 10. Because there are values that would normally be about the 5, the new graph just flattens out at the maximum.
14. The command find was used to create this code. Study the use of find (help find) and try to replicate the plot above. Provide your code.
t=linspace(0,4*pi/100,10);
y=10.*sin(100.*t);
plot(t,y,'r-o')
hold on
t2=linspace(0,4*pi/100,1000);
y2=10.*sin(100.*t2);
%plot(t2,y2,'k')
xlabel('Time (s)')
ylabel('y function')
legend('Coarse','Fine')
I=find(y2<5);
t3= t2(I);
y3= y2(I);
plot(t3,y3,'k')
To obtain the graph from 13, the above code was entered. the "find" code finds the indices of the values of a vector that are above or below a certain value. For this function, we used "find" to find the values for y2 that were less than 5, where y2 was the smooth function for 10sin(100t). With these indices found, we called these values to the new matrices of t3 for time and y3 for the y values of the function. Then we plotted y3 with respect to t3 to get the graph displayed above.
PART B: Filters and MATLAB
1. Build a low pass filter using a resistor and capacitor in which the cut off frequency is 1 kHz.
Observe the output signal using the oscilloscope. Collect several data points particularly around the cut off frequency. Provide your data in a table.
Frequency (Hz)
|
Output rms Voltage (V)
|
10
|
0.838
|
50
|
0.847
|
100
|
0.849
|
200
|
0.838
|
300
|
0.820
|
400
|
0.797
|
500
|
0.768
|
600
|
0.737
|
700
|
0.709
|
800
|
0.680
|
850
|
0.668
|
900
|
0.648
|
950
|
0.637
|
1000
|
0.625
|
1050
|
0.607
|
1100
|
0.599
|
1150
|
0.583
|
1200
|
0.573
|
1300
|
0.545
|
1400
|
0.516
|
1500
|
0.493
|
Table: Low pass filter frequency and resulting output voltage
*Input is 1 V peak to peak, or 0.707 rms V.
2. Plot your data using MATLAB. Make sure to use proper labels for the plot and make your plot line and fonts readable. Provide your code and the plot.MATLAB Code:
F=[10 50 100 200 300 400 500 600 700 800 850 900 950 1000 1050 1100 1150 ...
1200 1300 1400 1500]
Vout=[.838 .847 .849 .838 .820 .797 0.768 .737 .709 .680 .668 .648 .637 ...
.625 .607 .599 .583 .573 .545 .516 .493]
plot(F,Vout,'LineWidth', 3)
xlabel('Frequency (Hz)')
ylabel('rms Output (V)')
title ('Output Voltage Vs Frequency: Low Pass Filter')
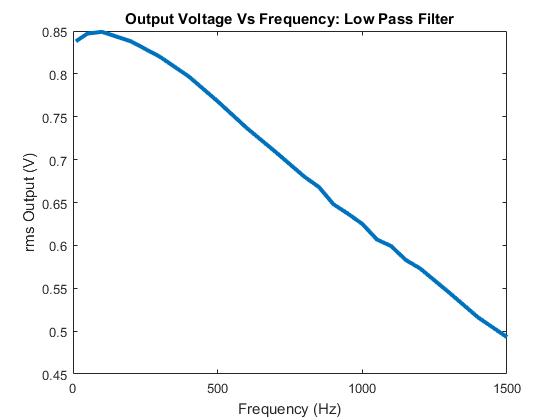
Graph: Low pass filter and resulting output voltage
3. Calculate the cut off frequency using MATLAB. find command will be used. Provide your code.
MATLAB Code:
F=[10 50 100 200 300 400 500 600 700 800 850 900 950 1000 1050 1100 1150 ...
1200 1300 1400 1500];
Vout=[.838 .847 .849 .838 .820 .797 0.768 .737 .709 .680 .668 .648 .637 ...
.625 .607 .599 .583 .573 .545 .516 .493];
plot(F,Vout,'LineWidth', 3)
xlabel('Frequency (Hz)')
ylabel('rms Output (V)')
title ('Output Voltage Vs Frequency: Low Pass Filter')
hold on
c=find(Vout<.707*.838);
d=c(1);
CutoffFrequency=F(d)
MATLAB Output:
CutoffFrequency =
1150
4. Put a horizontal dashed line on the previous plot that passes through the cutoff frequency.
Graph: Low pass filter frequency with respect to voltage
5. Repeat 1-3 by modifying the circuit to a high pass filter.
Frequency (Hz)
|
Output rms Voltage (V)
|
10
|
0.030
|
50
|
0.048
|
100
|
0.072
|
200
|
0.163
|
300
|
0.235
|
400
|
0.301
|
500
|
0.369
|
600
|
0.423
|
700
|
0.467
|
800
|
0.516
|
850
|
0.532
|
900
|
0.549
|
950
|
0.568
|
1000
|
0.582
|
1050
|
0.596
|
1100
|
0.610
|
1150
|
0.622
|
1200
|
0.634
|
1300
|
0.655
|
1400
|
0.678
|
1500
|
0.689
|
5.2.
MATLAB Code:
F=[10 50 100 200 300 400 500 600 700 800 850 900 950 1000 1050 1100 1150 ...
1200 1300 1400 1500];
Vout=[0.030 .048 .072 .162 .235 .301 .369 .423 .467 .516 .532 .544 .568 ...
.582 .596 .610 .622 .634 .655 .678 .689];
plot(F,Vout,'LineWidth', 3)
xlabel('Frequency (Hz)')
ylabel('rms Output (V)')
title ('Output Voltage Vs Frequency: High Pass Filter')
Graph: High pass filter frequency with respect to voltage
5.3 Calculate the cut off frequency using MATLAB. find command will be used.
F=[10 50 100 200 300 400 500 600 700 800 850 900 950 1000 1050 1100 1150 ...
1200 1300 1400 1500];
Vout=[.030 .048 .072 .162 .235 .301 .369 .423 .467 .516 .532 .544 .568 ...
.582 .596 .610 .622 .634 .655 .678 .689];
plot(F,Vout,'LineWidth', 3);
xlabel('Frequency (Hz)');
ylabel('rms Output (V)');
title ('Output Voltage Vs Frequency: Low Pass Filter');
x=find(Vout>.549);
c=F(s);
cutoff= min(c)
cutoff =
950




I noticed that you guys along with a number of other groups converted your pk to pk input and output values to rms values. I am beginning to realize this may be where my group made a mistake I thought that as long as we compared pk to pk values that our cutoff value should still be at .707*Vin. I am having trouble telling if you guys had the same cutoff frequency for your low pass filter as your high pass like we theoretically should have.
ReplyDeletei think you blog looks good but i am wondering how did you find the cut off frequency in the last question because i find it using different way
ReplyDeleteFor formatting wise, try highlighting or changing the color of the codes font for visibility purposes, I see you're missing some graphs from #1, 8, and 10. Other than that the graphs for the low/high filters and their cutoff values seem to be correct later in the blog.
ReplyDeleteYou seem to be missing some graphs in your blog so I would look into that. I suggest bolding the questions so it is easier to differentiate your answers from the questions. Everything we have for part A seems very similar to what you have. We used a higher input voltage peak to peak so our data is different. I am not sure where this confusion came from. Because of this, our graphs are not linear like everyone else’s.
ReplyDeleteno comments. Where are your graphs for part A?
ReplyDelete